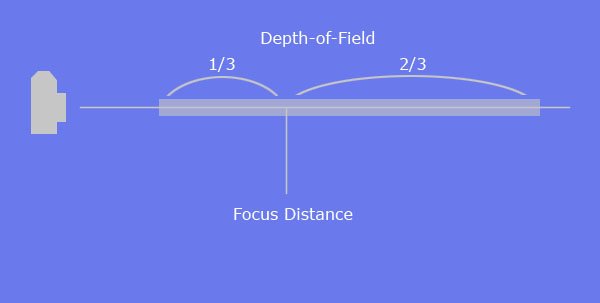
Je suppose que le titre et l'image expliquent bien ma question.
Pourquoi la zone de mise au point devant la distance de mise au point est-elle plus étroite que derrière?
Ce n'est pas le cas. Pas toujours. Juste généralement pour les photographes de paysage utilisant des objectifs plus larges visant un endroit pas si proche. :) La règle de proportion 1 / 3-2 / 3 est essentiellement une règle empirique qui ne s'applique pas dans tous les cas.
Plus votre ouverture est grande, plus votre objectif est long ou plus proche de votre distance de prise de vue (c'est-à-dire, plus la profondeur de champ est fine), plus cette proportion sera plus proche de 50/50 (pensez: distance hyperfocale).
Voir aussi:
-
http://www.cambridgeincolour.com/tutorials/depth-of-field.htm ( en particulier, le tableau montrant comment la distance focale fait varier la proportion avant / arrière dans la DoF.
-
http://www.photopills.com/articles/ultimate -guide-depth-field # step8
La profondeur de champ est une question d'angles et de pouvoir faire la différence entre eux. À mesure que les choses s'éloignent, les angles changent de moins en moins. Si vous avancez de 1 m à une distance de 2 m, vous pouvez modifier l'angle de 30 degrés. Si vous vous rapprochez de 1 m à une distance de 2000 m, l'angle ne change guère du tout.
La proportion de DoF proche et éloigné est le même principe, mais "compactée" autour du plan de meilleure mise au point.
Pourquoi la zone de mise au point devant la distance de mise au point est-elle plus étroite que derrière?
Ce n'est pas toujours le cas.
En fait, il est très rarement exactement un rapport 1: 2 comme illustré dans votre illustration. La règle d'or que vous avez citée n'est qu'approximative. Pour chaque distance focale et ouverture, il n'y a qu'une seule distance de mise au point précise où le rapport entre la profondeur de champ avant et arrière est exactement 1: 2.
Le rapport de la DoF devant le point de mise au point à la DoF derrière le point de mise au point sera différent pour chaque distance de mise au point lorsque vous utilisez le même objectif et le même réglage d'ouverture (en supposant que les autres conditions sont également les mêmes: grossissement / taille d'affichage, distance de vision, hypothèses sur la vision du spectateur, etc.).
À de courtes distances de mise au point, le rapport approche 1: 1. Un véritable objectif macro qui peut projeter une image virtuelle sur le capteur ou un film de la même taille que l'objet pour lequel il projette l'image atteint un rapport 1: 1. Même les objectifs qui ne peuvent pas réaliser la mise au point macro afficheront un rapport très proche de 1: 1 à leur distance de mise au point minimale.
Par exemple, en utilisant un téléobjectif de 300 mm avec un grossissement maximal de seulement 0,24X et un MFD de 59 pouces, le DoF calcule à 1: 1 dans les limites d'arrondi de la distance à un centième de pouce. Avec un appareil photo FF et un objectif 300 mm à f / 4, la DoF sera de 0,09 pouce devant la distance de mise au point et de 0,09 pouce derrière la distance de mise au point avec des conditions d'affichage et de visualisation standard. En réalité, la DoF proche sera microscopiquement plus petite que la DoF arrière. Cette différence n'est cependant pas perceptible et totalement dénuée de sens. Il faut augmenter la distance de mise au point à 133 pouces avant que la DoF proche à 0,54 pouces soit plus petite à deux chiffres significatifs que la DoF arrière à 0,55 pouces.
Avec un objectif 30 mm à f / 4, le rapport 1: 2 est obtenu à une distance de mise au point de 92 pouces. À la distance de mise au point macro pour un objectif 30 mm de 2,3622 pouces, le rapport est de 1: 1. Avec une distance de mise au point de 287 pouces (juste en dessous de la distance hyperfocale), le rapport est de 1: 61,4 avec une DoF proche de 141,2 pouces et une DoF éloignée de 8674,3 pouces.
À des distances de mise au point plus longues, l'arrière de la profondeur de champ atteint tout le chemin à l'infini et donc le rapport entre DoF avant et arrière approche 1: ∞. La distance de mise au point la plus courte à laquelle la DoF arrière atteint l'infini est appelée distance hyperfocale . La profondeur de champ proche approchera de très près la moitié de la distance de mise au point. Autrement dit, le bord le plus proche de la DoF sera à mi-chemin entre la caméra et la distance de mise au point.
Nous devons également nous rappeler que la distance hyperfocale, comme le concept de profondeur de champ sur lequel elle est basée, est vraiment juste une illusion, quoique plutôt persistante. Une seule distance sera au point le plus net. Ce que nous appelons la profondeur de champ sont les zones de chaque côté de la mise au point la plus nette qui sont si floues que nous les considérons toujours comme nettes. Veuillez noter que la distance hyperfocale variera en fonction d'un changement de l'un des facteurs qui affectent la DoF: distance focale, ouverture, grossissement / taille d'affichage, distance de visualisation, etc. Pour savoir pourquoi c'est le cas, veuillez consulter:
Pourquoi les fabricants ont-ils arrêté d'inclure les échelles DOF sur les objectifs?
Existe-t-il une «règle empirique» que je peux utiliser pour estimer la profondeur de champ pendant la prise de vue?
Comment déterminer le cercle de confusion acceptable pour une photo particulière?
Trouver la distance hyperfocale pour une résolution HD (1 920 x 1 080)?
Pourquoi j'obtiens des valeurs différentes pour la profondeur de champ des calculatrices par rapport à l'aperçu DoF intégré à l'appareil photo?
De même que cette réponse à la méthode simple d'estimation rapide de la DoF pour l'objectif principal
Vous avez raison, la DOF derrière le sujet est plus grande que la DOF avant lui, mais la différence peut être très petite. Que la distance derrière est plus grande peut être vu si vous regardez les formules pour DOF (de mhohner.de: Formules optiques):
Front DOF = cFd ^ 2 / (f ^ 2 + cFd)
DOF arrière = cFd ^ 2 / (f ^ 2-cFd)f est la distance focale
d est la mise au point (ou sujet) distance
F est le nombre F de l'objectif (2,8, 4, 5,6 etc.)
c est le cercle de confusion (généralement autour de 0,03 mm)
Vous voyez que le dénominateur pour le DOF arrière (f ^ 2-cFd) est toujours plus petit que le dénominateur pour le DOF avant (f ^ 2 + cFd), ce qui rend le DOF arrière plus grand.
Pour comprendre les objectifs et leur image, vous devez savoir que l'objectif projette une image du monde extérieur sur la surface d'un film ou d'un capteur numérique. Après un examen attentif, vous découvrirez que cette image est composée d'innombrables cercles de lumière. Ces cercles sont appelés cercles de confusion parce que leurs limites sont indistinctes et ils sont mélangés de bout en bout aux côtés d'innombrables cercles voisins.
Nous considérons qu'une image est nette lorsque ces cercles de formation d'image sont si petits que nous ne pouvons pas les percevoir comme des disques. Au lieu de cela, nous voyons un minuscule point de lumière qui n'est pas discernable en tant que disque. Cela équivaut à ½ millimètre vu à une distance de 500 mm. En d'autres termes, plus petit est meilleur.
Les rayons lumineux du sujet jouent sur la surface de l'objectif. Lorsqu'ils traversent la lentille, la forme de la lentille modifie leur trajectoire. Ils sont amenés à se plier vers l'intérieur (réfracter). Nous pouvons tracer ce chemin; il ressemble à deux cornets de glace fixés bout à bout pointu. Lorsque nous nous concentrons, nous ajustons la position de la surface du capteur numérique (ou du film) par rapport à l'objectif, de sorte que le sommet de ce cône de lumière embrasse simplement la surface sensible à la lumière. Si cela est réalisé, de petits cercles en résultent. Si la surface n'est pas exactement au sommet de ce cône, les cercles ne seront pas si petits. La netteté de l'image dépend du fait que ces cercles restent petits.
Désormais, la mise au point arrière (distance de l'objectif au plan de l'image) est une variable basée sur la distance du sujet. Si l'objet est à l'infini (aussi loin que l'œil peut voir), la mise au point arrière est à son plus court. Nous mesurons la longueur de la mise au point arrière lors de l'imagerie d'un objet à l'infini. Si l'objet est plus proche, la distance de mise au point arrière est allongée. Plus l'objet est proche, plus la mise au point arrière est longue. À l'unité (grandeur nature), la mise au point arrière est allongée à deux fois la distance focale. Si l'objet est juste timide de l'infini, la mise au point arrière n'est que légèrement allongée.
Voici ce que j'essaie de vous dire: la distance du sujet dicte la longueur de la mise au point arrière. À mesure que vous vous rapprochez de plus en plus du sujet, l'amplitude de l'élongation de la mise au point arrière augmente. L'essentiel est que les objets éloignés de la caméra ont presque la même distance de mise au point arrière sur une plage étendue. À l'inverse, les objets proches de la caméra ont une mise au point arrière étendue, et cette distance change radicalement avec les changements de distance. Ce sont ces changements de mise au point qui changent la taille du cercle de confusion. Le résultat est le suivant: la profondeur de champ s'étend d'environ 2/3 vers l'avant et 1/3 vers l'arrière vers la caméra à partir du point focalisé.
La réponse courte est:
Parce que c'est une relation exponentielle.
La réponse longue ... (pas si longue) est que vous n'utilisez pas d'unités de dimension linéaire comme 1 mètre, mais des proportions.
Votre image ne dit pas que le milieu est au centre de 2 mts = 1 mt.
Cela indique que vous avez le double de la distance.