La déclaration de mattdm " ce flou est largement réversible si vous faites exactement la même chose à l'envers" a soulevé la question dans mon esprit. La rotation est une transformation géométrique de l'image qui consiste en une transformation spatiale des coordonnées et une interpolation d'intensité. Si la rotation n'est pas un multiple de 90 degrés, alors l'algorithme d'interpolation joue un rôle crucial.
Dans de tels cas, si nous utilisons un algorithme d'interpolation de moyenne (par exemple, bicubique), l'opération est avec perte * . Mais pouvons-nous utiliser une approche différente (par exemple, l'interpolation du voisin le plus proche) à la place et avoir notre image tournée "sans rotation"?
(*) Ce n'est que mon sentiment (je ne peux toujours pas le supporter avec une preuve mathématique): comme on ne peut pas savoir avec certitude quel pixel a contribué à quelle valeur, on ne peut pas inverser le moyennage. Mais je ne suis pas sûr que nous ne puissions pas utiliser de méthodes probabilistes pour estimer avec précision les valeurs originales.
Bien que je ne dispose pas des compétences mathématiques requises, j'ai moi-même effectué des tests (avec gimp ), mais après anti-rotation, les images diffèrent:
Test 1

Figure 1 - Image source (256x256)
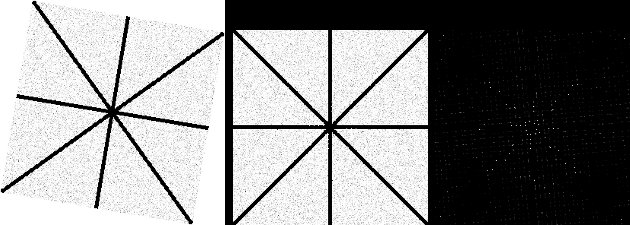
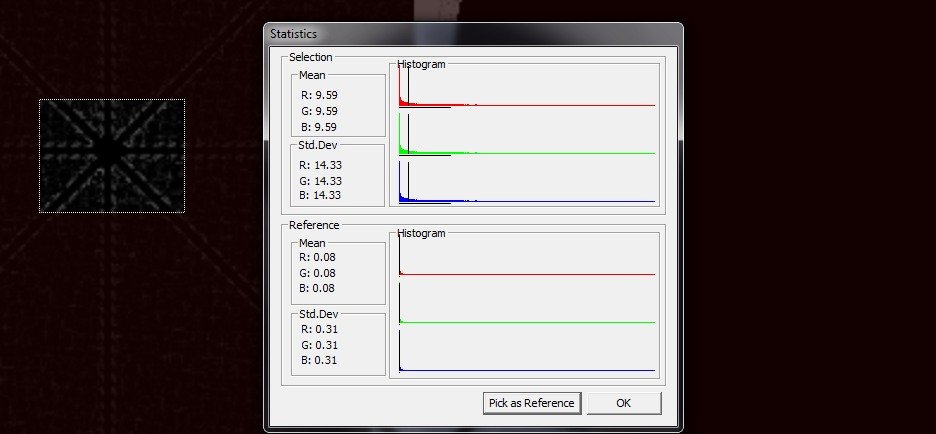
Figure 2 - De gauche à droite: a) image tournée de 9,5 degrés dans le sens des aiguilles d'une montre; b) image tournée à nouveau de 9,5 degrés dans le sens anti-horaire; et c) différence entre les images. Pour ces opérations, j'ai utilisé l'interpolation le plus proche voisin . Les images sont réduites après les opérations pour mieux s'adapter à la mise en page de ce site Web.
Test 2
Suite à la suggestion de @ unapiedra, j'ai fait un test plus simple: faire tourner une matrice 2x2. Ce cas n'est pas intéressant car, selon l'angle, soit toutes les cellules sont tournées du même angle, soit aucune cellule n'est tournée. Autrement dit, la rotation est toujours sans perte.
J'ai donc réessayé avec une matrice 3x3 et une rotation de 30 degrés:
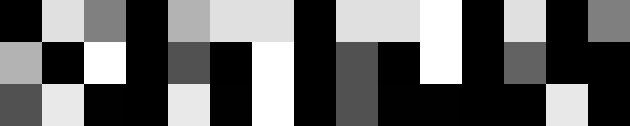
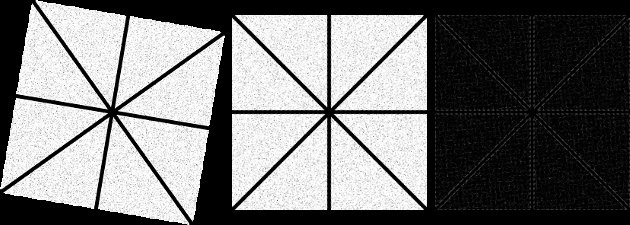
Figure 4 - De gauche à droite: a) image source; b) image tournée de 30 degrés dans le sens des aiguilles d'une montre; c) image tournée de 30 degrés dans le sens inverse des aiguilles d'une montre; d) différence. Les images sont mises à l'échelle pour s'adapter à ce site Web.
Dans ce cas, les différences sont évidentes. La rotation est clairement avec pertes ... Mais que se passe-t-il si je monte à l'échelle avant la rotation?
Test 3

Figure 5 - De gauche à droite: a) image source; b) image mise à l'échelle d'un facteur 6x; c) image mise à l'échelle tournée de 30 degrés dans le sens des aiguilles d'une montre; d) image tournée de 30 degrés dans le sens inverse des aiguilles d'une montre; e) image transformée réduite; et f) différence (pas de différence). Les images sont mises à l'échelle pour s'adapter à ce site Web.
Dans ce cas, je mets à l'échelle par un facteur 6x. Raisonnement pour choisir ce facteur (malheureusement incorrect comme je l'ai vu avec un contre-exemple):
Un pixel pivoté à 30 degrés a des coordonnées de bas-gauche à haut-droite: [0,0] - [0,3660 , 1,3660]. Autrement dit, le côté projeté le plus court a une longueur de 0,36 pixels. Le théorème d'échantillonnage exige que nous échantillonnions à un taux double.
Ainsi, pour échantillonner avec précision une image pivotée de 30 degrés, je dois échantillonner chaque 0,17 pixel, ce qui donne un redimensionnement x5,88 facteur; 3 x 5,88 = 17,64, donc je rééchantillonne l'image source en une image 18x18.