Premièrement, la distance est utilisée pour la distance focale car elle mesure la distance entre le plan de la lentille et le point de rencontre des rayons réfractés en un point, lorsque les rayons incidents étaient parallèles. Voici un schéma simple d'une seule lentille. Remarque: Ceci est uniquement pour les lentilles convexes.

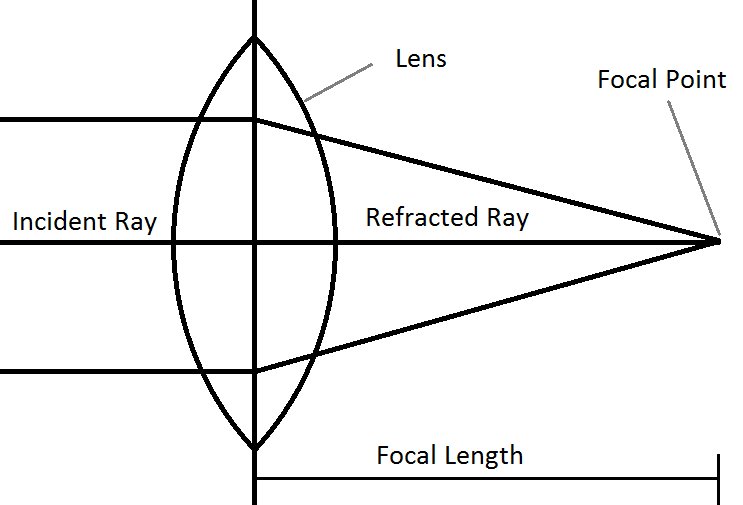
L'utilisation des millimètres est simplement parce que c'est une échelle appropriée pour cette mesure. c'est-à-dire que les longueurs les plus extrêmes ne deviennent pas des nombres trop grands ou trop petits pour que nous les comprenions facilement. Théoriquement, toute mesure de longueur ou de distance peut être utilisée, mais cela devient impossible. Par exemple, un objectif de 50 mm pourrait également être considéré comme étant d'environ 5,28511705 × 10 ^ -18 années-lumière ou 0,0005 km. Ces deux mesures sont extrêmes mais valides, mais pas pratiques.

Pourquoi pas des centimètres? De nombreux objectifs ont des distances focales qui ne sont pas des centimètres entiers, et si possible, il vaut mieux représenter un nombre sans point décimal, et donc mm est une unité plus pratique. Il y a certainement une raison historique / traditionnelle aussi.

Les objectifs de caméra fonctionnent sur le même principe que l'objectif simple simple, mais incluent de nombreux éléments pour la mise au point et le téléobjectif.

Parce que dire que vous avez un objectif .0002485 furlong est beaucoup plus encombrant que d'appeler le même objectif "50 mm".

Les distances focales des objectifs courants se trouvent être dans la plage de sorte que le mm entier fonctionne bien. Les chiffres ne deviennent ni trop grands ni trop petits, et 1 mm est inférieur à la précision qui nous intéresse habituellement, mais pas trop. En d'autres termes, c'est une unité pratique.

Bien qu'elle soit utilisée pour exprimer le champ de vision, la distance focale d'un objectif est une distance réelle - la distance à laquelle une image focalisée est formée à partir de rayons parallèles. En tant que telle, n'importe quelle unité de distance peut être utilisée - si vous regardez des objectifs vraiment anciens, vous la trouverez souvent indiquée en pouces. La plupart des pays du monde ont maintenant adopté le système métrique, c'est donc ce qui est utilisé (pour des raisons de normalisation, la plupart des fabricants de lentilles sont également basés en Europe ou en Extrême-Orient). Ils auraient pu choisir des centimètres ou des mètres, mais cela aurait impliqué d'utiliser des décimales.

Il se trouve que le millimètre est juste assez fin pour spécifier toutes les distances focales courantes sous forme de nombres entiers.

L'autre façon logique de caractériser un objectif pourrait être par l'angle FOV qu'il produit.

Nous n'aurions plus besoin de penser en "équivalences 35 mm", mais nous aurions besoin de changer la désignation du lentille en fonction de la taille de la monture / du capteur sur laquelle elle est utilisée. Il semble donc que l'indication de la distance focale (dans n'importe quelle unité) soit plus pratique, car elle ne change pas si un objectif est utilisé sur un boîtier moyen format, plein cadre, apsc de 4: 3.

Et nous aurions également besoin de convenir au préalable si l'angle est mesuré horizontalement, verticalement ou en diagonale également. Et puis si on le mesure en degrés ou en radians!

Le point sur la pertinence de la taille de l'unité est bien compris, cependant, tout comme les polices sont mesurées en points (qui sont 1/72 de pouce), la longueur focale aurait bien pu être mesurée dans une certaine mise à l'échelle d'un pouce qui a donné des nombres tout aussi bien comportés. Je pense que l'utilisation du millimètre est venue du fait qu'un tas de bricolages précoces avec la photographie a été fait en Europe, en particulier en France qui venait d'adopter le système métrique et donc les premiers techniciens ont opté pour le mm, plutôt que pour une fraction de pouces. Cependant, je n'ai aucune source pour cette conjecture.