Quand j'ai commencé la photographie, celui-ci m'a pris du temps à comprendre, car les gens ont tendance à l'expliquer avec beaucoup de mathématiques, ou d'une manière qui a du sens une fois que vous avez déjà compris le principe, mais pas avant.

Comment le facteur de recadrage affecte-t-il la perspective?

Ce n'est pas le cas.

Pas du tout, du tout.
La seule façon de changer de perspective est de déplacer la caméra.
Changer le boîtier ou l'objectif n'a aucun effet sur la perspective.
Cela n'affecte que la part de l'image globale que vous pouvez voir à travers le viseur.

Il a été un tel succès la dernière fois qu'il est apparu, je le ramène pour un encore.
L'ours en peluche ... & la bibliothèque

^{J'ai triché en les faisant pour qu'ils ne se superposent pas parfaitement; J'ai utilisé un objectif zoom, assorti à l'œil dans le viseur & plus tard recadré pour s'adapter au mieux - appelez cela licence artistique juste pour démontrer rapidement un point;)
Cliquez sur n'importe quelle image pour une version plus grande.}

Voici notre héros sur une caméra à cadre recadré avec un objectif 85 mm

Sans changer la position de la caméra, permutez l'appareil photo mais pas l'objectif.
85 mm en plein format

OK, ça a l'air complètement différent - mais ce n'est pas un changement de perspective, vous pouvez simplement voir plus car le capteur est plus grand.

Prouvez-le en superposant une image sur l'autre ...

Encore une fois, sans bouger la caméra, passez à 120 mm [environ] sur la caméra FF. Vous verrez une image identique à notre première photo - à l'exception de la différence de profondeur de champ, qui sera légèrement moins profonde. La perspective du cadrage d'& sera identique.

La superposition est assombrie pour afficher une image incrustée de 120 mm au-dessus de notre image 85 mm d'en haut - c'est difficile à dire, mais ce n'est pas une superposition parfaite de l'image précédente, probablement en raison de la nature très approximative de ma méthode ainsi que le changement de DOF.

Ensuite, pour terminer l'expérience, revenez à l'objectif 85 mm sur le FF .
Nous pouvons maintenant déplacer la caméra jusqu'à ce que nous recadrions l'ours comme il l'était dans la photo "héros" depuis le début.

Maintenant, nous avons changé de perspective, en déplaçant la caméra.
Même si nous avons recadré pour correspondre à l'ours dans notre photo d'origine, l'ours superposera presque parfaitement la première photo , sauf pour le changement de perspective - l'arrière-plan est maintenant totalement différent.

Pas correct. La perspective (se référant à la taille et à l'espacement des objets d'arrière-plan par rapport au sujet) est déterminée uniquement par la distance de l'appareil photo au sujet. Il s'agit de la géométrie tirée de la position de la caméra, quels que soient les détails de la caméra.

Une autre distance focale ou une autre taille de recadrage de la caméra (et un agrandissement ultérieur à une taille équivalente) peut "agrandir la taille de tout ce qui est vu", mais ne peut voir que la même vue avec la même perspective si vous vous trouvez au même endroit à la même distance . Penser juste une seconde conclura que c'est évident. Nous ne pouvons pas voir deux vues différentes à partir du même endroit. La perspective ne dépend que de l'endroit où nous nous trouvons pour la voir.

Nous imaginons que de longues lentilles compressent la distance, si nous changeons également de place, pour nous tenir loin en arrière, à une distance différente. Mais si vous vous trouvez au même endroit, l'agrandissement d'une image à partir d'une distance focale plus courte ne peut nécessairement voir que la même vue exacte à partir du même endroit. Cette vue est tout ce que l'on peut voir à partir de cet endroit.

Par rapport au sujet, se tenir à un endroit avec un objectif, vs se tenir 3 fois plus loin avec un objectif 3x plus long, les deux verront la même chose vue du sujet et champ (au sujet). Nous appelons cela une vue équivalente (en parlant du sujet et de sa distance et de sa zone de champ à sa distance). Cependant, l'arrière-plan le plus éloigné dépendra de la position de la caméra. Se tenir plus en arrière avec un objectif plus long verra moins d'arrière-plan, même si la vue est le même champ sur le sujet. C'est une propriété très précieuse à connaître pour les portraits en extérieur, pour recadrer et minimiser les arrière-plans gênants (elle offre également un peu plus de profondeur de champ à la distance du sujet).

Encore une fois, la perspective dépend uniquement de la distance de la caméra, c'est-à-dire de l'endroit où vous vous trouvez pour la voir.

1. La perspective est la taille des objets de l'image par rapport les uns aux autres - elle est déterminée par leur distance de la caméra et les uns des autres dans la scène.

2. La composition est la totalité du contenu de l'image, l'emplacement des objets et leurs tailles par rapport à la taille de l'image , certains incluent également la perspective comme un sous-ensemble de composition.

3. La distance focale est une propriété géométrique / optique d'une lentille, mesurée en unités de distance.

4. La taille du cadre, aussi appelée «format», est une propriété de la caméra (et informe également sur la conception de l'objectif car un objectif doit pouvoir la satisfaire en projetant une image suffisamment grande) - elle est mesurée le long de la diagonale de l'image en unités de distance.

5. Le recadrage consiste à modifier la taille du cadre, soit en utilisant un autre appareil photo, une zone de capteur, un dos numérique, un film, ou en recadrant numériquement une image plus grande.

6. Le champ de vision et son angle de vue correspondant sont déterminés par le distance focale par rapport à la taille du cadre - elle peut être modifiée en modifiant l’un des deux par rapport à l’autre.

7. Changement du champ de vision (soit en un / recadrage, soit en changement de distance focale aka zoom) sans déplacer la caméra ou la scène n'affecte pas la perspective, cela affecte la composition car les objets sont inclus ou exclus du cadre et la taille des objets existants par rapport à la taille de l'image change.

8. Pour maintenir une composition donnée sous un changement de champ de vision (si on n'inclut pas de perspective dans la définition de composition sinon on dit que c'est impossible et on passe à 9.), disons garder le cadre rempli avec le visage du sujet dont vous avez besoin pour éloigner ou rapprocher l'appareil photo du sujet - cela modifie la perspective et, dans le cas de portraits, les proportions perçues des traits du visage.

9. Pour créer une image identique à la fois en perspective et en composition (une image «équivalente») avec des tailles d'image différentes, le même champ de vision doit être conservé, car les tailles d'image sont données, cela signifie changer la focale longueur. De combien ? En le multipliant par le rapport entre l'ancienne et la nouvelle taille d'image, c'est le facteur de recadrage et c'est pourquoi il est également connu sous le nom de «multiplicateur de distance focale» - il ne multiplie pas la distance focale d'un objectif donné, la distance focale de un objectif donné est multiplié par lui pour obtenir une nouvelle distance focale nécessaire pour qu'une image équivalente soit créée sur une taille de cadre différente.

"Comment le facteur de recadrage affecte-t-il la perspective?"

Le film Super 35 a généralement une taille d'image de 24,89 mm x 18,66 mm, ce qui est plus petit qu'un appareil photo FF (36 mm x 24 mm), mais plus grand qu'un appareil photo de recadrage Canon (22,5 mm x 15 mm) ou un appareil photo de recadrage Nikon (24 mm x 16 mm).

Cela suppose un rapport hauteur / largeur de 3: 2 pour les images fixes, mais la vidéo DSLR utilise un 16 : 9 et je ne suis pas sûr de la taille d'image exacte utilisée dans les vidéos 16: 9.

La taille de l'image vidéo et le facteur de recadrage vont changer considérablement en fonction de la caméra et de la résolution avec lesquelles vous photographiez. (Le Canon 5D Mk IV a un facteur de recadrage de 1,74 lors de la prise de vue vidéo 4K)

Source de l'image

Dans En général, si vous utilisez un capteur d'image plus petit (capteur de recadrage), vous devez soit vous tenir plus en arrière, soit utiliser un objectif plus large (focale plus courte) pour obtenir le même cadrage du sujet.

Se tenir plus en arrière changera la perspective, mais en utilisant un objectif plus large et en se tenant plus près, vous devriez pouvoir faire correspondre la perspective.

Je pense que dans la plupart des cas, Super 35 et la vidéo APS-C sont suffisamment proches pour que la personne moyenne ne puisse pas faire la différence.

Point de vue en termes de caméra - plus que vous ne le pensez:

Tout d'abord une qualification - Sauf dans des circonstances particulières, une perspective correcte (correcte) n'a pas d'importance pour la grande majorité des photos prises. Cependant, c'est la propriété de perspective de l'image bidimensionnelle qui permet au spectateur de porter des jugements sur les distances englobées. Pour certaines imaginations, une perspective correcte ou presque correcte est essentielle. Nous parlons d'imagerie scientifique et d'imagination flatteuse de visages, etc.

Perspective correcte: si vous regardez par une fenêtre, vous pouvez tracer avec un crayon de cire, les contours des objets, sur la vitre. Une telle trace révèle le «juste» ou la «perspective humaine». Nous pouvons dupliquer cette perspective si nous remplaçons l'œil humain par une caméra. La taille (format) de l'appareil photo ou la combinaison d'objectifs à focale utilisée ne font aucune différence.

Nous pouvons voir cette photo car elle offrira une perspective «correcte» si elle est vue de la même taille (impression de contact ou image de la même taille que la puce d'imagerie), à ​​une distance égale à la distance focale de la prise lentille. Dans les temps modernes, une telle distance de vision est problématique car nos caméras produisent des images miniatures et la distance focale utilisée est probablement plus courte que notre distance de lecture naturelle. Il est donc probable que l'image résultante s'agrandisse. Supposons que nous agrandissons à 8 X 12 pouces pour la visualisation. Cela nécessitera un grossissement de 8 ½ X si la caméra est un format plein format 35 mm. Si l'appareil photo est un appareil photo numérique compact (APS), le grossissement requis sera de 12 X. En d'autres termes, chaque taille de format différente dicte le grossissement requis pour créer une image de taille finale affichée.

Revenons maintenant à la perspective «correcte»: si l'image de la caméra n'est pas agrandie et vue à une distance égale à la distance focale de l'objectif de prise de vue, la perspective réalisée est «correcte». S'il est agrandi, nous devons réviser la distance de vision en fonction du grossissement appliqué. Supposons que l'objectif 50 mm soit monté sur un plein cadre et qu'une image 8 X 12 soit affichée en agrandissant l'image de la caméra 8,5X. Maintenant, la distance de visualisation est de 8,5 X 50 mm = 425 mm = 17 pouces. Si ces conditions sont remplies, le spectateur est présenté avec une perspective «correcte».

Supposons que la même vue soit imagée à l'aide d'un numérique compact avec un objectif de 30 mm monté. Le grossissement pour obtenir une image 8 X 12 est de 12X. La distance de visualisation qui offre une perspective «correcte» est de 33 X 12 = 396 mm = 16 pouces.

Conclusion: le format ou la distance focale ne fait aucune différence à condition que l'image soit vue à une distance égale à la distance focale de l'objectif de prise multipliée par le degré d'agrandissement.

Un point clé: la plupart des images sont vues à une distance à peu près égale à leur diagonale. Ce fait est pris en compte par la coutume de l'industrie d'attribuer la distance focale «normale» pour un format basé sur la mesure diagonale. Pour le plein cadre, cette valeur est de 45 mm mais généralement arrondie à 50 mm pour convaincre. Pour le numérique compact (APS), cette valeur est d'environ 33 mm

Un dernier point: au fil des ans, les tailles des caméras ont diminué en raison des améliorations technologiques apportées aux capteurs de film et d'imagerie. Cette tendance se poursuivra. La distance focale de la lentille expédiée également réduite proportionnellement. Ainsi, la perspective finale de l'image est un entrelacement de taille de format, de distance focale, de distance de vision et de grossissement pour créer l'image qui sera visualisée.

Non.

LA PERSPECTIVE EST TOUJOURS CONCERNANT LA POSITION DE LA CAMÉRA PAR RAPPORT AUX SUJETS VISIBLES DANS LE CHAMP DE VISION. IL NE S'AGIT JAMAIS DE L'OBJECTIF, DE LA TAILLE DU CAPTEUR OU DE QUELQUE CHOSE D'AUTRE.

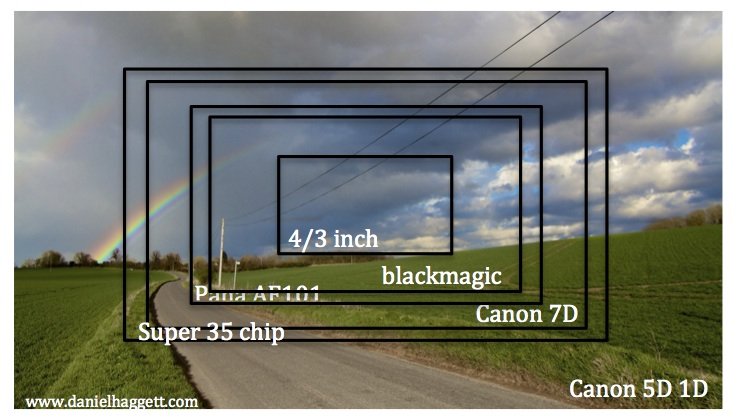
Pour autant que je sache, photographier la même image sur l'appareil photo APS-C que l'appareil photo Super 35 besoin d'utiliser un objectif plus large, la distance focale nécessaire étant déterminée par le facteur de recadrage. Cependant, en utilisant une lentille plus large, cela affecterait la perception de la profondeur, par ex. les objets d'arrière-plan apparaissent plus loin qu'ils ne le font lors de l'utilisation d'un objectif plus long. Cela ne donnerait donc pas la «même» image. Est-ce correct?

NON IL N'EST PAS. SI LA CAMÉRA EST DANS LA MÊME POSITION, ELLE A LA MÊME PERSPECTIVE. PERIODE. ¹

Les parties de la scène qui sont visibles dans une image seront visibles dans l'autre. Les parties de la scène masquées par d'autres objets de la scène seront toujours masquées par ces autres objets. En effet, les lignes de la caméra à chaque objet sont toujours les mêmes et sont toujours droites. Ce qui peut changer, c'est la façon dont ces objets sont projetés par l'objectif, ce qui affectera la forme de ces objets tels qu'ils sont projetés sur le plan focal, mais les mêmes parties de chaque objet seront visibles et les mêmes parties ne seront pas visibles tant que le la caméra et les objets sont tous dans la même position. Voilà ce qu'est la perspective !

Toute différence entre deux images réalisées avec des objectifs différents prises à partir de la même position et avec le même champ de vision ne sera PAS due à des différences de perspective. Ils seront dus aux différences entre les deux objectifs en termes de projection géométrique causées par la façon dont chaque objectif réfracte la lumière qui le traverse, par la résolution absolue différente des deux systèmes objectif / caméra, par la différence de couleur et de transmission de la lumière entre les deux systèmes caméra / objectif, etc. Mais il n'y aura aucune différence de perspective si les deux photos sont prises exactement à la même position.

La différence entre une image prise avec un fisheye 8 mm et une image prise avec un objectif rectiligne 8 mm n'est pas une différence de perspective si les deux images sont prises à partir de la même position de prise de vue. C'est une différence dans la géométrie de la projection d'un monde 3D sur un capteur (ou film) 2D. S'il y a deux objets là-bas avec une partie d'un objet devant une partie de l'autre objet, tant que vous tirez à partir du même endroit exactement, les mêmes parties exactes de l'objet arrière seront vues et les mêmes parties de l'objet arrière seront masquées par l'objet le plus proche . Voilà ce qu'est la perspective !

La différence dans la façon dont ces deux objets sont de forme différente sur les deux photos n’est pas une perspective , c’est une géométrie de projection . Deux choses totalement différentes. La distorsion de perspective est le résultat de la position de prise de vue. La distorsion géométrique est le résultat des différentes façons dont différents objectifs projettent la même perspective sur un capteur d'image plat ou un morceau de film.

Pour en savoir plus, veuillez voir cette réponse à une question différente mais connexe: Y a-t-il une différence entre une prise de vue de loin avec un objectif 50 mm et une prise de vue rapprochée avec un objectif 35 mm?
Voir cette réponse à: Le grand angle équivaut-il dans l'image du capteur de recadrage à biaiser l'image?

La perspective dépend uniquement de la distance de prise de vue - à la fois la distance de l'appareil photo au sujet et la distance entre l'appareil photo et le premier plan / arrière-plan, et les rapports entre eux tous. Si vous photographiez à la même distance avec deux tailles de capteur différentes ou des distances focales différentes et que vous recadrez la photo la plus large pour qu'elle corresponde à l'angle de vue le plus étroit, la perspective est identique .

Si vous photographiez à partir de la même position avec les deux caméras, prenez la caméra Super 35 et recadrez-la au même angle de vue du capteur APS-C qui vous donnera à peu près la même image, à part les différences de qualité optique entre les deux capteurs et résolution perdue lors du recadrage.

Mais même si vous photographiez avec le même appareil photo, la prise de vue à une distance différente donnera une perspective différente. En effet, la distance de prise de vue est la seule chose qui détermine la perspective. La distance focale et la taille du capteur déterminent alors l'angle de vue et le cadrage à partir de cette distance de prise de vue. Donc, la sauvegarde avec un capteur de recadrage pour obtenir le même cadrage du sujet qu'un capteur plus grand à une distance de prise de vue plus rapprochée donne également une perspective différente: les tailles et formes relatives des éléments plus proches et plus éloignés de l'appareil photo changeront comme le rapport entre les distances des différents éléments et la caméra change.

_{Copyright de l'image 2007 SharkD, sous licence CC-BY-SA 3.0}

Voici un exemple extrême des différences d'effet de distance de prise de vue lorsque vous utilisez différentes focales pour obtenir le même cadrage à différentes distances. Le changement de perspective est dû au changement de distance de prise de vue et aux différents rapports de distance entre les différents éléments de la scène et la caméra lorsque la caméra avance et recule pour préserver le cadrage du sujet à différentes distances focales.

https://imgur.com/XBIOEvZ

Comment pouvons-nous nous assurer qu'une image équivalente est capturée, à la fois en termes de champ de vision et de perspective?

Photographiez à partir de la même position exacte avec une combinaison objectif + caméra qui donne la même chose angle de vue. C'est si simple. Si vous voulez la même profondeur de champ, appliquez également le rapport entre les tailles de capteur / focales de l'objectif et le nombre f utilisé.

_{¹ La raison pour laquelle nous réfléchissons une distance focale plus large rend les objets en arrière-plan plus petits qu'ils ne le seraient si nous avions utilisé un objectif à focale plus longue parce que lorsque nous utilisons un objectif plus large nous nous rapprochons du sujet . Cela modifie le rapport entre la distance caméra-sujet et la distance arrière-plan de la caméra. Si nous photographions un sujet à une distance de 15 pieds et que l'arrière-plan est encore à 15 pieds derrière le sujet, le rapport des distances par rapport à l'appareil photo est de 1: 2 (15 pieds / 30 pieds). Si nous utilisons un objectif plus large et que nous nous déplaçons à moins de 1,50 mètre du sujet, le rapport est maintenant de 1: 4 (5 pieds / 20 pieds).}

Pour plus d'informations, veuillez consulter: Pourquoi avez-vous besoin de changer votre position plutôt que simplement la distance focale pour affecter la perspective?
Quelle est la différence entre la distorsion de perspective et la distorsion en barillet ou en coussin? Y a-t-il une différence entre une prise de vue de loin avec un objectif 50 mm et une prise de vue rapprochée avec un objectif 35 mm?
Le grand angle équivaut-il à une image biaisée du capteur de recadrage?
Distance focale sur les cadres pleins et les capteurs recadrés
Un téléobjectif peut-il avoir un large champ de vision?
Comment la distance focale changer de perspective?
Pourquoi l'arrière-plan est-il plus grand et plus flou dans l'une de ces images?
Qu'est-ce que cela signifie vraiment que les téléobjectifs "aplatissent" les scènes?

Briser le mythe: perspective & de longueur focale