La règle des tiers est une simplification du nombre d'or. Fondamentalement, si vous mettez quelque chose sur la troisième ligne comme l'œil d'une personne ou quelque chose sur un horizon, la composition de l'image sera souvent conforme au nombre d'or.

Le nombre d'or se produit souvent dans la nature comme les coquilles de conque ou d'escargot, les pétales de fleurs, etc. Depuis son identification (ou sa définition) par les Grecs, il a été fréquemment utilisé dans l'art et l'architecture depuis.

Un professeur de design d'une école de design danoise nous a donné un cours de doctorat sur la composition de nos présentations PowerPoint scientifiques. Il a également mentionné que nous ne devrions jamais placer deux personnages côte à côte, mais un ou trois. Il a également utilisé un exemple de bougies 2 vs 3. Il a fait valoir que cela avait à voir avec la façon dont nos yeux se déplacent lors de l'inspection de la scène.

S'il y a deux moitiés, les yeux vont faire un ping-pong d'avant en arrière, sans jamais trouver de repos. Un point principal laissera les yeux se reposer sur cela, et trois feront inspecter les yeux un par un et se reposer sur le plus proéminent. Ce qui signifie que non seulement vous devez faire une division par trois, mais également composer la scène de manière à ce qu'il y ait une partie dominante pour attirer l'attention, et vous assurer que les autres parties sont complémentaires.

De nos jours, les gens aiment ça faites des recherches sur la manière dont nous inspectons les images, mais M. Smith a mentionné dans Qu'est-ce que la «règle des tiers»?, il était douteux qu'une telle recherche soit disponible au 18e siècle. Peut-être ont-ils trouvé la raison plus tard de ce qu'il a trouvé intuitivement.

L'autre ligne directrice de Smith sur le fait de ne pas avoir deux lumières également proéminentes dans la scène correspond à la théorie du concepteur.

La règle des tiers n'a rien à voir avec une «loi» scientifique: c'est juste une ligne directrice, une règle empirique. La question de savoir si une photo prise en l'utilisant est «meilleure» qu'une autre sans est subjectif.

Ce n'est également qu'une des nombreuses directives similaires telles que le nombre d'or et la division de la scène en triangles. C'est à vous, en tant que photographe, de décider de ce qui vous convient le mieux.

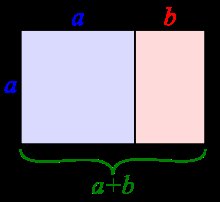
Il y a beaucoup de science derrière le nombre d'or (section d'or), dont la règle des tiers est une simple approximation. Le rapport (connu sous le nom de phi) d'environ 1,618 se produit maintes et maintes fois dans la nature et les mathématiques.

La question est de savoir s'il y a une science derrière l'esthétique de ce rapport. Bien sûr que cela se produit dans la nature, les Grecs pensaient que le rapport était beau, etc., mais y a-t-il une preuve réelle derrière cela? Il semblerait très difficile de prouver scientifiquement quelque chose qui est subjectif, et la recherche ne semble pas concluante.

Une étude de peintures célèbres conclut:

Une étude statistique sur 565 œuvres d'art de différents grands peintres a été réalisée et il a été calculé le rapport des 2 faces d'un tableau. En supposant que tous les peintres en discussion entrent dans une statistique à poids égaux, on montre que la valeur moyenne obtenue pour le rapport des côtés est de 1,34. Cette valeur, déterminée expérimentalement, est significativement différente de la valeur de la section d'or F = 1,618, qui est un rapport théorique, obtenu à partir d'une théorie mathématique abstraite, qui devrait supposément imprimer sur un tableau une harmonie suprême

Fechner, Godkewitsch et Benjafield ont mené des études où les sujets ont été invités à classer divers rectangles en fonction de l'attractivité. Ces études se contredisent, mais dans l'ensemble, il semble y avoir une préférence pour les rectangles dont les côtés sont proches du nombre d'or.

Le Dr Mario Livio, un scientifique et fanatique d'art, a écrit un article sur le sujet, et conclut:

L'histoire de l'art a néanmoins montré que les artistes qui ont produit des œuvres d'une valeur réellement durable sont précisément ceux qui se sont écartés de tout canon formel pour l'esthétique

J'écris actuellement un mémoire sur ce sujet et sur l'utilisation des grilles de composition en général. Sur la base de mes recherches, il existe des preuves que la règle des tiers et des grilles phi est esthétique, mais la relation avec les règles de composition et l'esthétique est beaucoup plus compliquée que la simple mise en page sur une grille de proportions. Cela a à voir avec la relation entre la symétrie et l'asymétrie et la façon dont nous la percevons.

Par exemple, les compositions dites statiques sont généralement en corrélation avec des compositions symétriques et horizontales plates qui semblent centrées ou équilibrées, que la mise au point soit centrée ou équilibré sur une grille de composition. La règle des tiers, le nombre d'or / grille phi a à voir avec la rupture de symétrie et la compensation de la composition. Cela dit, un plan de système de grille se lit toujours avec certains éléments de symétrie à la manière de la gestalt. L'interaction entre asymétrie (décalage) et symétrie est le véritable objectif des règles de composition et des grilles.

Il y a des mathématiques impliquées, qui est le sujet de ma thèse, mais cela varie en fonction du rapport hauteur / largeur de l'image et de sa hauteur ou de sa largeur. Considérez les systèmes de grille comme un cadre pour créer un récit de symétrie / asymétrie dans la composition. À cet égard, la règle des tiers est le système le plus «généralement» utile car il peut s'adapter à n'importe quel rapport hauteur / largeur de manière prévisible. Les grilles Phi peuvent mieux fonctionner en fonction de la largeur de l'image et de son contenu. En général, les images orientées verticalement correspondent moins souvent aux règles parce que la composition a tendance à se lire horizontalement plutôt que verticalement, en d'autres termes, moins d'espace horizontal signifie moins de lecture compositionnelle. L'exception évidente concerne les compositions orientées en diagonale qui se lisent aussi bien dans les deux sens.

La chose principale à regarder est la symétrie / asymétrie et non la grille. La grille renforce l'attente de symétrie, tandis que la composition décalée joue sur l'idée de briser la symétrie avec l'asymétrie, ce que notre motif reconnaissant les cerveaux adore, d'où l'attrait esthétique des œuvres.

Il est possible que nous soyons conditionnés à trouver des images composées avec la règle des tiers plaisantes ou "correctes". Il est très important dans les œuvres d'art historiques, l'architecture &, la photographie moderne, le design, etc. J'ai même vu des gens critiqués pour ne pas l'avoir suivi lors de concours photo. Il pourrait être considéré comme sacré simplement en raison de son conditionnement et de son utilisation, et non à cause d'une propriété inhérente qui lui soit propre. Je ne sais pas si je commence ici un truc entier de poulet et d’œuf.

Cela n'a pas été seulement commencé par des photographes. c'était le début des peintres de la Renaissance. Le voulait composer de manière à ce que le sujet puisse être placé sans interférer avec l'arrière-plan. Ils voulaient montrer des arrière-plans également en dehors du sujet. Et ils ont découvert que normalement nos yeux ne tombent pas sur le centre de la toile. il erre sur les côtés de la toile. Et c'est ainsi que les artistes ont commencé à diviser le canevas en 3 colonnes et n lignes, et la règle est entrée en vigueur.

Il n'y a pas besoin d'explication scientifique pour la règle des tiers, car c'est un fait.
Vous avez probablement vu l'image de l'Homme de Vitruve dessinée par Leonardo da Vinchi. Ce dessin est parfois appelé Canon de proportions . Pourquoi cette image nous intéresse-t-elle? En fait, il est basé sur des proportions humaines idéales, et c'est une très bonne source pour comprendre les proportions et les mettre en œuvre non seulement dans le dessin, mais aussi dans l'architecture, le design, l'image, la statuaire, etc.
Par exemple: le maximum la largeur des épaules correspond au quart de la hauteur d'un homme. Mieux vaut y parvenir dans votre composition d'image, vos images seront meilleures. Et ce n'est pas seulement lié aux proportions humaines, c'est lié à la nature, aux humains, aux choses, etc.