L'équation suppose une simple lentille à élément unique qui est bilatéralement symétrique. L'objectif de la caméra, pour atténuer les 7 aberrations majeures (lacunes qui se dégradent), est construit à l'aide de plusieurs éléments de lentille en verre individuels. Certains ont une puissance positive, d'autres une puissance négative. Certains sont espacés par l'air et certains sont cimentés ensemble. Parce que ce tableau devient assez complexe, le point à partir duquel nous mesurons la distance focale sera probablement décalé du centre physique du barillet de l'objectif.

Dans une conception de téléobjectif véritable, le nodal arrière (point de mesure) est décalé vers l'avant. Cette action raccourcit la longueur du barillet de l'objectif, ce qui rend l'appareil photo et l'objectif moins difficiles à tenir, à utiliser et à ranger. Dans certains modèles, le nodal arrière peut en fait tomber en l'air devant le barillet de l'objectif.

Comme le dit l'équation: à l'unité (grossissement 1), la distance du sujet est de 2 longueurs focales vers l'avant et la mise au point arrière est de 2 focales derrière le nodal arrière. Le problème est --- vous ne pouvez pas localiser facilement le nodal arrière. Cependant, une fois le grossissement de 1 atteint, vous pouvez désormais mesurer la distance sujet à image. De nombreuses caméras fournissent un symbole (cercle coupé en deux avec une ligne) sur le cadre de la caméra; pour localiser la position du plan image.

Dans tous les cas, mesurez la distance sujet à image et divisez par 4. Cette division révèle la distance focale. Divisez par 2 et cette division localise le point nodal arrière. Vous êtes désormais mieux équipé pour utiliser la «formule du fabricant d’objectifs».

Tout d'abord, félicitations pour vos efforts pour décomposer un problème de photographie en principes fondamentaux.

L'écart que vous avez observé provient d'une simplification excessive courante. Votre objectif 100 mm est en fait ce que les ingénieurs optiques appellent un «assemblage d'objectif» Comme vous le savez probablement, il est composé de plusieurs éléments d'objectif en groupes travaillant en tandem pour former, affiner et transmettre l'image vue. par votre capteur d'image.

Si votre ensemble d'objectif de 100 mm se composait d'un seul élément d'objectif de 100 mm, vous auriez des distorsions massives et seuls le rouge, le vert ou le bleu pourraient être mis au point à la fois, mais mince L'équation de grossissement de l'objectif que vous avez liée serait vraie. Un agrandissement de 1 serait obtenu lorsque le sujet est à 200 mm du point nodal et que l'ensemble de lentilles devrait avoir une longueur physique supérieure à 200 mm. Même dans ce cas, cela ne serait strictement précis que dans la mesure où l'équation de la lentille mince est appropriée (et ce n'est pas particulièrement approprié ici.) Une bonne réponse proviendrait d'une dérivation du fabricant de lentilles. équation

Un corollaire de la différence entre un assemblage et une lentille mince est les points nodaux bilocalisés. Une lentille mince a un emplacement unique pour les points nodaux avant et arrière; Les deux sont colocalisés avec la pupille d'entrée. Si tel était le cas pour votre objectif, vous seriez capable de l'objectif libre en tournant autour de l'ouverture de votre objectif sans aucune parallaxe avec le sujet ou le capteur. Je suis sûr que si vous essayez cela avec la macro 100 mm, vous constaterez que ce n'est pas vrai. Une lentille épaisse a deux points nodaux qui ne sont colocalisés que si son indice net est de 0, c'est-à-dire. il n'a pas de focale. Un ensemble de lentilles peut être approché par une lentille épaisse virtuelle avec deux indices idéalisés de telle sorte que la lentille virtuelle a les mêmes sommets, longueurs focales relatives, pupille d'entrée et (de manière saillante) points nodaux que l'ensemble de lentilles.

Pour plus de crédit, vous pouvez consulter la description d'un objectif composé et essayer de deviner quelles combinaisons de focales d'objectif créeraient la situation que vous avez décrite. NB le "grossissement du télescope". C'est essentiellement ce que fait un concepteur d'objectifs.

Pour plus d'informations, vous pouvez consulter les différents types de conceptions d'objectifs photographiques

La plupart des objectifs à focale fixe font la mise au point en modifiant leur distance focale en plus de déplacer le ou les points nodaux de l'objectif. Pour faire la mise au point sur un objet proche de l'appareil photo, l'objectif réduit sa distance focale. Un objectif spécifié comme «100 mm» est généralement «100 mm lorsqu'il est mis au point à l'infini», mais pas nécessairement lorsqu'il est mis au point sur un objet rapproché.

Il y a deux raisons pour lesquelles la distance sujet à image n'est pas de 40 cm au grossissement unitaire:

1. la distance focale de l'objectif peut ne pas être de 100 mm
2. la distance entre les plans principaux peut ne pas être nulle.

Laquelle de ces raisons est la plus importante est impossible à dire sans informations détaillées sur la conception optique de la lentille.

Distance focale

La valeur «100 mm» inscrite sur l'objectif lui-même est une distance focale nominale , qui est normalement une valeur arrondie de la focale réelle distance lorsque l'objectif est mis au point à l'infini.

Certains objectifs, généralement appelés objectifs à «mise au point unitaire», réalisent la mise au point en déplaçant l'ensemble optique dans son ensemble. Ces lentilles ont une distance focale qui ne varie pas avec la mise au point. Cependant, de nombreux objectifs complexes, y compris pratiquement tous les objectifs macro modernes, ont une sorte de «correction de portée rapprochée» (dans le langage Nikon): leurs formules optiques changent au fur et à mesure que vous faites la mise au point, ce qui permet une meilleure correction des aberrations. vous faites la mise au point.

Ces deux faits: l'arrondissement de la distance focale nominale et le fait qu'elle varie lorsque vous faites la mise au point signifient que vous ne savez pas quelle est la distance focale réelle de l'objectif au grossissement unitaire.

Plans principaux

La page Wikipedia que vous citez définit d _o et d _i comme la distance de l'objectif à l'objet (resp. image ), mais notez que ces définitions apparaissent dans une section consacrée spécifiquement aux thinlenses. Votre lentille étant une lentille composée épaisse, cela soulève la question de l'applicabilité de la formule.

Il s'avère que l'approximation de la lentille mince n'est pas applicable dans cette situation. Cependant, la formule est toujours valable si elle est interprétée dans le contexte du modèle lentille épaisse . Dans ce modèle, le plan de la lentille mince est remplacé par deux plans, appelés «plans principaux»:

• le «front» (ou «primaire», ou «Côté objet») le plan principal est utilisé pour mesurer les distances dans l'espace objet
• le plan principal «arrière» (ou «secondaire», ou «côté image») est utilisé pour mesurer les distances dans l'espace image

Ces sont des plans conjugués avec un grossissement unitaire. Dans la figure ci-dessous ( source), ce sont les plans verticaux qui passent par H ₁ , N ₁ et H _{2 sub >, N 2 :}

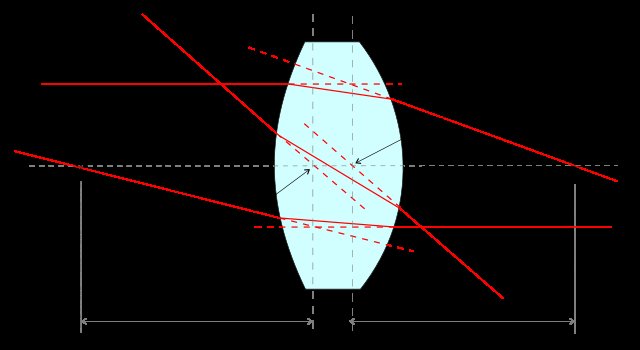
Notez que cette façon de décrire un système optique en fonction de ses points cardinaux (le F _i , H _i et N _i ci-dessus) est également applicable aux lentilles composites. Voir par exemple cet ancien dessin d'un téléobjectif ( source) où les deux plans principaux (les plans verticaux passant par N _i et N _o ) sont à gauche côté de l'élément le plus à gauche:

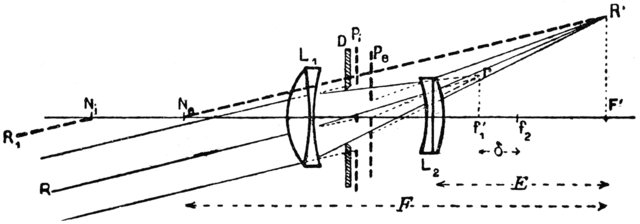
Ainsi, votre formule est toujours valide à condition de définir:

• d _{o comme la distance du sujet au plan principal principal}
• d _i comme la distance du plan principal secondaire à l'image

Cela donne la distance sujet-image comme

d _o + e + d _i = 4f + e

au grossissement unitaire, où e est la distance (éventuellement négative) entre les plans principaux. Notez que la lentille mince indique approximativement que les plans principaux sont coïncidents (e = 0), mais cela ne s'applique pas à votre cas.

Pour plus d'informations sur ce sujet, vous pouvez jeter un œil à:

• cette courte vidéo sur les principaux avions
• ces notes de cours sur les lentilles épaisses

L'idée fausse de l'objectif mince

J'ai écrit cette réponse principalement pour aider à dissiper une idée fausse populaire, qui apparaît dans certaines des réponses ici, y compris celle que vous avez acceptée: qu'un objectif photographique équivaut à un objectif mince .

Il s'avère que dans la plupart des situations photographiques (essentiellement toutes les situations non macro), la distance sujet-objectif est beaucoup plus grande toute distance caractéristique de la lentille elle-même. Dans de telles situations, le point de référence que vous utilisez pour mesurer la distance au sujet n'a pas vraiment d'importance. Il convient alors d'oublier la distance qui sépare les plans principaux et de considérer que le plan arrière-principal est le seul qui compte. Cela équivaut à régler e = 0, qui est essentiellement l'approximation de la lentille mince.

S'en tenir à cette approximation rend l'apprentissage de l'optique beaucoup plus simple, car vous n'avez pas besoin de comprendre des notions telles que les plans principaux, les points principaux ou nodaux , espace objet, espace image, etc. Considérant que:

• l'approximation est assez bonne pour la plupart (non macro) fins
• les connaissances en optique ne sont utiles qu'à un photographe qualitativelevel, car vous n'allez pas concevoir d'objectifs et vous n'avez pas besoin d'expertise en optique pour devenir un grand photographe

il est compréhensible que l'objectif fin soit le modèle le plus couramment enseigné aux photographes. Et pourtant, l'approximation se rompt lorsqu'il s'agit d'une lentille épaisse complexe à des distances macro. Les réponses qui vous disent que la distance focale est un quart de la distance sujet-image illustrent comment cette idée fausse conduit les gens à poster de fausses réponses.

La distance de travail est mesurée de l'avant de l'objectif au sujet. Pour votre objectif macro EF 100 mm f / 2,8 L IS USM, la distance de travail à distance de mise au point minimale (MFD) / grossissement maximal est d'environ 133 mm.

La distance de mise au point est mesurée à partir du sujet au plan d'imagerie (film ou capteur). Pour votre objectif macro EF 100 mm f / 2,8 L IS USM, la distance de mise au point à grossissement maximal / MFD est de 300 mm.

La distance focale de la plupart des objectifs est mesurée lorsque l'objectif est mis au point à l'infini (puis arrondi au focale "standard" la plus proche). Lorsque la distance de mise au point est réduite, l'angle de vue fourni par l'objectif change souvent. C'est ce que l'on appelle la respiration focalisée . Le MFD 300 mm de votre EF 100 mm f / 2,8 L IS USM Macro nous révèle que la distance focale effective à un grossissement de 1: 1 est d'environ 75 mm. Ceci est assez courant pour un objectif macro avec une distance focale comprise entre 90 et 105 mm. Le Tamron 90 mm f / 2,8 Di VC USD Macro (F017), par exemple, a également un MFD de 300 mm à un grossissement de 1: 1.

De plus, la distance focale pour un objectif composé est approximée à partir de la distance focale une seule lentille devrait fournir le même grossissement. Une lentille composée est un système de plusieurs lentilles, généralement disposées en groupes, qui agissent ensemble comme une seule lentille. Presque tous les objectifs disponibles dans le commerce pour les systèmes de caméras à objectifs interchangeables sont des objectifs composés. Votre EF 100 mm f / 2,8 L IS Macro dispose de 15 éléments d'objectif disposés en 12 groupes.

Pour la plupart des objectifs grand angle dotés d'une conception rétrospective, ce point théorique simple d'objectif unique est bien derrière l'avant de l'objectif . Pour les téléobjectifs, ce point est, par définition, devant l'avant de l'objectif.

Lorsque la mise au point est effectuée à la distance minimale de mise au point (MFD) de 300 mm, l'avant de votre EF 100 mm f / 2,8 L IS USM Macro se trouve à environ 168 mm devant le capteur. Mais le champ de vision et le grossissement fournis par l'objectif au MFD en font effectivement un objectif de 75 mm à cette distance de mise au point. Cela signifie qu'un simple objectif de 75 mm devrait être à 150 mm devant le capteur (ce qui place également à 150 mm du sujet) pour un grossissement de 1: 1. Cela place le point central effectif de votre macro EF 100 mm f / 2,8 à environ 18 mm derrière l'avant de l'objectif lorsqu'il est mis au point sur le MFD.

Je pense donc qu'il me manque quelque chose, quelqu'un peut-il expliquer où je Je me trompe?

Lorsque vous appliquez des formules telles que celles de votre question, vous devez utiliser 75 mm pour la distance focale de l'objectif lorsqu'il est mis au point sur MFD.